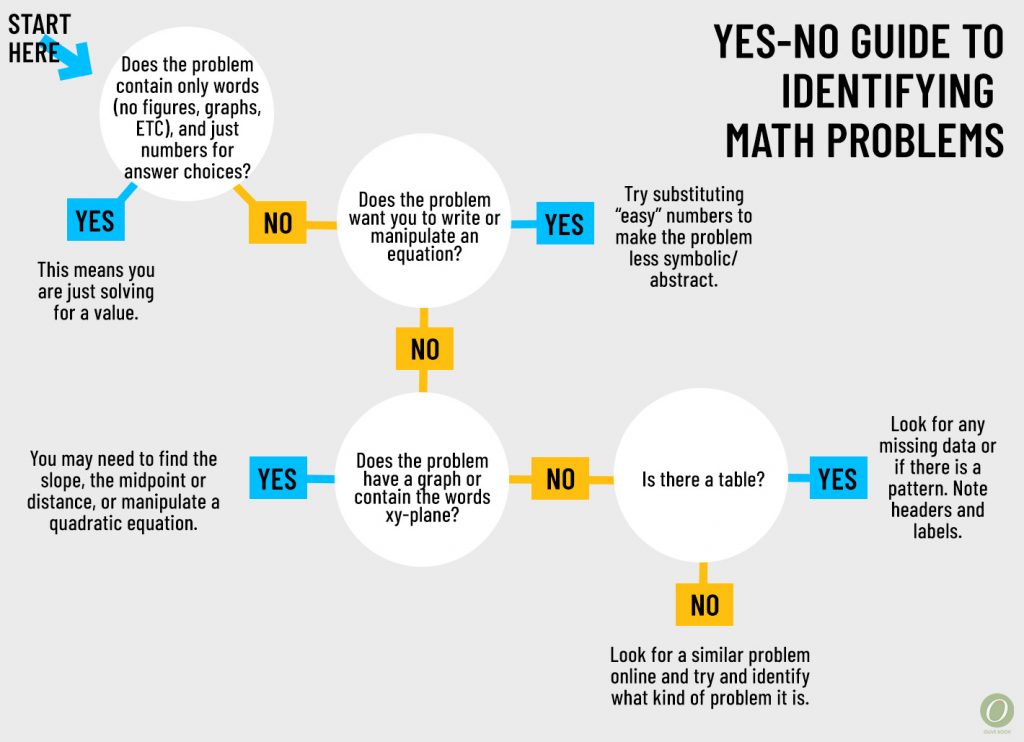
In our past Math section strategy posts, we’ve talked about the importance of recognizing what kind of math problem you’re looking at in order to recall how to solve it. However, most classroom situations don’t require you to practice this kind of problem solving and it does take some practice, just like any other skill you want to improve! So we wanted to provide four math section strategies for practicing recognizing math questions as you see them.
Since there are so many topics covered on the ACT and SAT Math tests, we simplified the long list by instead examining what the problems are actually asking. Understanding what the problems are asking can clue you into what kind of math problem it is.
Below, you’ll find a list of cues to use to diagnose the problem, tips for solving, and a few sample problems for each cue!
1. Does the problem want you to write or manipulate an equation?
Pay Attention to:
- The answer choices – you will notice that these multiple-choice questions have variables in the answers.
- The wording of the question – the question might say in terms of or which is equivalent to.
To prepare for these types of questions:
- Practice translating word problems to algebraic expressions or equations.
- Take given equations and try to write them to solve for a different variable.
If you really get stuck on the test:
- Try substituting “easy” numbers to make the problem less symbolic/abstract and instead something more concrete that makes sense to you.
Sample Math Problems:
(Answers at end of the post)
1. You have m amount of money in your wallet. After you spend s amount on new shoes, what percent of the original amount of money is left in your wallet in terms of m and s?

2. The equation h = -2t2+vt+r gives the height h of a foam rocket at t seconds after it is launched with an initial velocity of v from a roof height of r feet. Which of the following is equivalent to v in terms of h, t, & r?
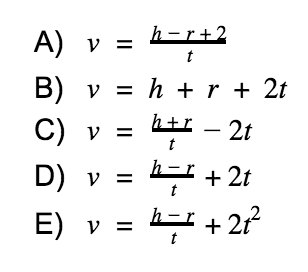
2. Does the problem have words with no figures, graphs or tables, and just numbers (no variables) for answer choices (or in the case of the SAT, no answer choices at all)? This means you are just solving for a value.
Pay attention to:
- If it is a function problem or one that can be solved by simply replacing a variable with a numeric value given in the problem.
- Whether or not you may need to solve the problem by translating the words to an algebraic equation to solve.
- If there are two “sets” of information that might require you to write and solve it as a system of equations.
- Words such as mean, median, mode, and range.
To prepare for these types of questions:
- Make sure you know the order of operations and how to manipulate negative numbers and/or exponents.
- Practice translating word problems to algebraic expressions or equations.
- Make sure you understand how to interpret a table and graph in function notation. The x-value is inside the parenthesis and the f(x) is the y-value.
- Try problems that could be solved by finding patterns in the numbers or sequences that may need to be extended.
- Practice tricky word problems that use central tendency.
If you really get stuck on the test:
- As it is a multiple choice problem, try working backwards by substituting in the answer choices. Start with the answer choice in the middle, that way if it is incorrect you can just try a higher or lower value without having to try every answer choice.
Sample Math Problems:
3. Which of the following is NOT a solution to the inequality 2x+6>4x-2?

4. If y>0 and x = 8 in the equation:
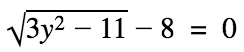
what is the value of y?

5. At a food truck, one taco costs $1.50 less than a chicken quesadilla. If you and a friend order 4 tacos and 2 quesadillas, and the cost is $24, how much does a chicken quesadilla cost?

3. Does the problem have a graph or contain the words xy-plane?
Pay attention to:
- A graph with straight lines, or the word linear because it is most likely asking you to find the slope, x-intercept, y-intercept, or mid-point if it is just one line. Or, it may ask about a line that is parallel, perpendicular, the point of intersection, or number of solutions if it is referring to two lines.
- Whether or not the word parabola, x-intercepts, vertex, maximum or minimum are in the question. Then you know you are dealing with a quadratic which looks like a parabola when graphed.
- If there is a circle (or other conic) or the words radius, diameter, or center are in the question. Then you may have to identify the equation of the circle or length of the diameter or radius.
- Whether the graph has many “curves” because you will likely have to identify the zeros, or x-intercepts.
To prepare for these types of questions:
- Be sure you know all you know how to find the slope, all your linear forms, and how to find the midpoint or distance.
- Know that parallel lines have the same slope and share no solutions, except when they are actually the “same line” in which case they have infinite solutions. Perpendicular lines have slopes that are negative reciprocals, and a bisector “cuts” a line directly in half.
- Practice changing quadratic equations between standard form, factored form, and vertex form. Also practice graphing the quadratics in their different forms.
- Translate graphs vertically and horizontally, and for quadratics (parabolas) transform the width. Notice how transformations affect the equations.
If you really get stuck on the test:
- If no graph is given, try a quick sketch graph. Or if you are really stumped, make an xy-table and try values to see what happens to the graph.
Sample Math Problems:
6. When graphed in the xy-plane, which of the following shares no solutions with -5x-2y=20?
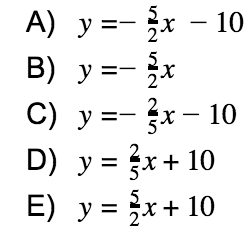
7. When graphed in the xy-plane, which of the following functions has zeros (x-intercepts) at -2 and 6?
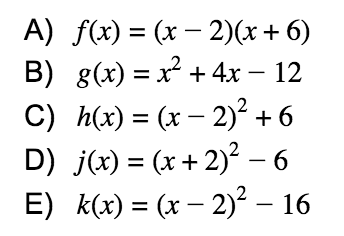
8. A parabola with a vertical axis has its vertex at the origin and passes through the point (2,2). The parabola intersects the line y=8 at two points. What is the length of the segment joining these two points?

4. Does the problem have a table?
Pay attention to:
- The title and the labels on the rows and columns, and if there is a scale such as “data is shown in thousands.” Also notice if the word frequency is a label. This points to a question about mean, median, or standard deviation.
- Whether or not totals are given at the end of each row or the bottom of each column. The presence of totals means this question will most likely ask about probability or proportions as either fractions or percentages.
- Any missing data because the question is probably going to ask you to supply it.
- If there is a pattern in the numbers in the table. This means the question will most likely deal with linear or exponential growth or decay.
To prepare for these types of problems:
- Practice finding the mean in a frequency table. Understand that the closer the data is to the mean, the lower the standard deviation. The more spread out the data means the standard deviation will be greater. Know how an outlier affects the mean, median, and range.
- Be sure you can recognize whether a probability is comparing a part to a part, or a part to the whole.
- Know common fractions and their percent equivalents or how to mentally set up a proportion to have 100 as a denominator. This will save time because you won’t need a calculator.
- Understand the difference between a linear pattern, and one that is exponential. Would the data go in a straight line when graphed, or would it make a curve?
If you really get stuck on the test:
- Work backward. Look at each answer choice and compare it to the data in the table. Eliminate answer choices that obviously don’t make sense.
- When data are large numbers, round or estimate to make the problem easier to do mentally.
Sample Math Problems:
9. A history teacher has two 20-student sections of World History. At the end of the semester he created tables to show the grade point distribution between the two sections. Note: A = 4, B = 3, C = 2, D = 1, F = 0.
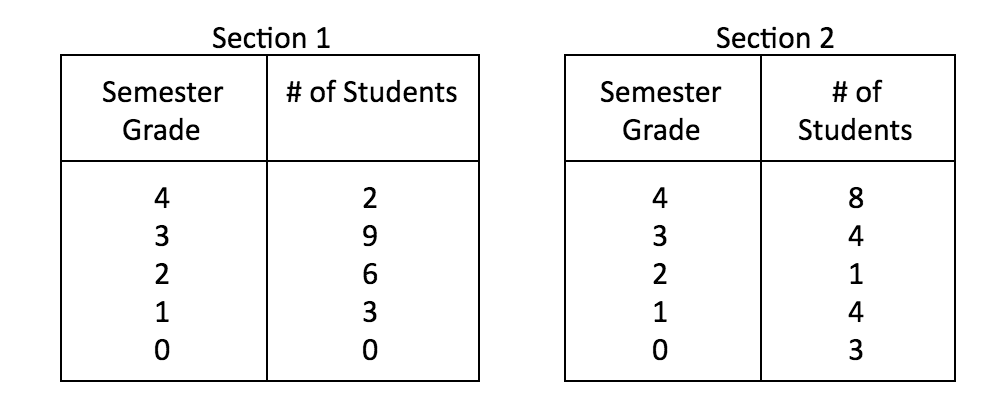
Which of the following statements best describes the data for the given year?

10. Below is data from a survey of 400 people who were asked about their hand preference and whether or not they were a twin or a not a twin.
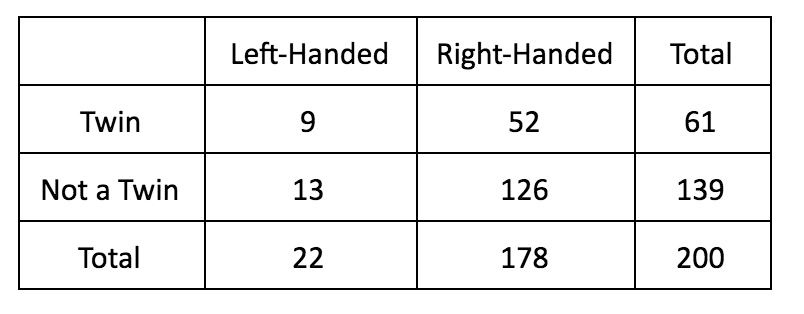
According to the data, what is the probability, to the nearest percent, that a randomly selected person from this group is left-handed or a twin?

Becoming proficient in math problem recognition is important to your overall math section practice. It not only helps you answer questions correctly, but it also helps you identify why you get certain questions wrong! And once you know why you got a question wrong, you know what to practice during your next study session.
More resources:
ACT Math Strategies
SAT Math Strategies
ACT/SAT Math Vocabulary Terms to Know
Formulas on the ACT Math Section
SAT Math Formulas to Know
Answers
1. C 2. D 3. E 4. E 5. E 6. B 7. E 8. C 9. D 10. D
